Segitiga Siku-siku: Keistimewaan, Sudut, dan Perhitungannya

Dalam kehidupan sehari-hari, banyak hal menggunakan konsep segitiga, terlebih segitiga siku-siku. Misalnya pada bidang arsitektur, teknik sipil, pelayaran, dan navigasi penerbangan. Oleh karena itu, perhitungan-perhitungan terkait segitiga siku-siku mestinya dipahami sehingga dapat lebih mudah menyelesaikan masalah sehari-hari yang berkaitan dengan penerapan segitiga siku-siku.

Segitiga siku-siku adalah segitiga yang salah satu sudutnya siku-siku atau 90°. Ciri lain segitiga siku-siku adalah sebagai berikut.

Segitiga siku-siku memiliki dua sisi yang saling tegak lurus.
Sudut siku-siku berada pada perpotongan sisi-sisi yang tegak lurus.
Sisi di depan sudut siku-siku adalah sisi miring (hipotenusa).
Berlaku teorema Phytagoras, yaitu "Kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang sisi-sisi siku-sikunya".

Keliling Segitiga Siku-siku

Keliling segitiga siku-siku dapat dihitung dengan cara menjumlahkan panjang ketiga sisinya.

$K=AB+BC+AC$

Luas Daerah Segitiga Siku-siku

Luas daerah segitiga siku-siku pada gambar di atas dapat dihitung dengan mengalikan setengah panjang sisi alas dan tingginya, atau sebagai berikut.

$\boxed{L=\frac{1}{2}\times alas\times tinggi}$

atau

$\boxed{L=\frac{1}{2}\times BC\times AC}$

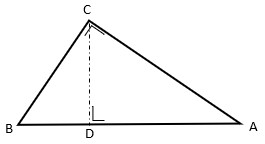
Sementara luas daerah segitiga pada gambar berikut ini, dapat dihitung dengan cara:

$L=\frac{1}{2}\times BC\times AC=\frac{1}{2}\times AB\times CD$

Teorema Phytagoras

Kuadrat panjang sisi miring sama dengan jumlah kuadrat panjang sisi-sisi siku-sikunya.

Klik untuk melihat Pembahasan teorema Phytagoras.

Contoh Soal

Contoh 1

Segitiga ABC adalah segitiga siku-siku di titik A. Jika luas daerah segitiga ABC adalah 32 cm² dan panjang garis AB adalah 8 cm, berapakah panjang sisi-sisi yang lain?

Jawab.

Diketahui : $L=32 cm^{2}, AB=8$ cm.

Ditanya : $AC$ dan $BC$

Berikut ini gambar segitiga ABC.

Menghitung panjang sisi AC:

\begin{array}{rcl} L& = &32 \\ \frac{1}{2}\times AC\times AB&=&32\\ \frac{1}{2}\times AC\times AB&=&32\\ \frac{1}{2}\times AC\times 8&=&32\\ 4\times AC&=&32\\ AC&=&\frac{32}{4}\\ AC&=&8 \end{array}

Menghitung panjang sisi BC:

\begin{array}{rcl} BC^{2}&=&AB^{2}+AC^{2} \\ BC^{2}&=&8^{2}+8^{2}\\ BC^{2}&=&64+64\\ BC^{2}&=&128\\ BC&=&\sqrt{128}\\ BC&=&8\sqrt{2}\\ \end{array}

Jadi, panjang sisi AC adalah $8$ cm dan BC adalah $8\sqrt{2}$ cm.

Contoh 2.

Segitiga PQR adalah segitiga sama sisi dengan panjang sisi 10 cm. Berapakah luas daerah segitiga PQR?

Jawab.

Berikut ini adalah gambar segitiga PQR.

Menghitung tinggi segitiga PQR:

\begin{array}{rcl} PS^{2}&=&PR^{2}-RS^{2} \\ PS^{2}&=&10^{2}-5^{2}\\ PS^{2}&=&100-25\\ PS^{2}&=&75\\ PS&=&\sqrt{75}\\ PS&=&5\sqrt{3}\\ \end{array}

Menghitung luas daerah segitiga PQR:

\begin{align} L&=\frac{1}{2}\times alas\times tinggi\\ &=\frac{1}{2}\times QR\times PS\\ &=\frac{1}{2}\times 10\times 5\sqrt{3}\\ &=5\times 5\sqrt{3}\\ &=25\sqrt{3}\\\end{align}

Jadi, luas daerah segitiga PQR adalah $25\sqrt{3}$ cm.

Contoh 3.

Perhatikan gambar kubus berikut. Kubus ABCD.EFGH memiliki panjang rusuk 10 cm. Hitunglah panjang garis AC dan AG!

Jawab.

Berikut ini tampilan garis AC dari sudut yang berbeda.

Dari gambar di atas, kita bisa melihat segitiga ABC siku-siku di titik B, sehingga dapat diterapkan teorema Phytagoras.

\begin{array}{rcl} AC^{2}&=&AB^{2}+BC^{2} \\ AC^{2}&=&10^{2}+10^{2}\\ AC^{2}&=&100+100\\ AC^{2}&=&200\\ AC&=&\sqrt{200}\\ AC&=&10\sqrt{2}\\ \end{array}

Berikutnya akan dihitung panjang garis AG dengan bantuan segitiga ACG. Perhatikan gambar berikut.

Segitiga ACG merupakan segitiga siku-siku di titik C, sehingga berlaku teorema Phytagoras.

\begin{array}{rcl} AG^{2}&=&AC^{2}+CG^{2} \\ AG^{2}&=&200+10^{2}\\ AG^{2}&=&200+100\\ AG^{2}&=&300\\ AG&=&\sqrt{300}\\ AG&=&10\sqrt{3}\\ \end{array}

Jadi, panjang garis $AC=10\sqrt{2}$ cm dan $AG=10\sqrt{3}$ cm.

Latihan

Segitiga PQR adalah segitiga siku-siku di titik Q. Jika luas daerah segitiga PQR adalah 24 cm² dan panjang garis QR adalah 6 cm, berapakah panjang sisi-sisi yang lain?
Segitiga DEF adalah segitiga sama sisi dengan panjang sisi 8 cm. Berapakah luas daerah segitiga PQR?
Kubus ABCD.EFGH memiliki panjang rusuk 8 cm. Hitunglah panjang garis BD dan BH!