Menghitung Panjang Diagonal Sisi dan Diagonal Ruang Kubus

Diagonal adalah garis melintang yang menghubungkan dua titik sudut yang berseberangan. Kubus memiliki dua jenis diagonal, yaitu diagonal sisi ⟮diagonal bidang⟯ dan diagonal ruang. Bagaimana menghitung panjang diagonal sisi dan diagonal ruang pada kubus? Simak artikel ini sampai akhir agar dapat memahami caranya.

Diagonal Sisi

Diagonal sisi adalah garis yang menghubungkan dua titik sudut yang berseberangan pada bidang yang sama. Perhatikan kubus berikut.

Diagonal sisi pada kubus ABCD.EFGH pada gambar di atas adalah AC, BG, dan DE. Coba, sebutkan diagonal sisi yang lainnya!

Contoh 1. 

Hitunglah panjang diagonal sisi AC pada kubus ABCD.EFGH yang memiliki panjang rusuk 8 cm!

Penyelesaian.

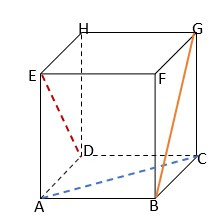
Berikut ini gambar kubus ABCD.EFGH dan diagonal sisi AC.

Diagonal AC berada pada sisi ABCD. Perhatikan segitiga ABC.

Dengan menerapkan teorema Phytagoras, diperoleh

\begin{array}{rcl} AC^{2}&=&AB^{2}+BC^{2} \\ AC^{2}&=&8^{2}+8^{2}\\ AC^{2}&=&64+64\\ AC^{2}&=&128\\ AC&=&\sqrt{128}\\ AC&=&8\sqrt{2}\\\end{array}  

Jadi, pajang diagonal sisi AC adalah $8\sqrt{2}$ cm.

Dengan cara yang sama, jika panjang rusuk kubus adalah $a$, maka diperoleh panjang diagonal sisi kubus adalah:

$\boxed {a\sqrt{2}}$

Diagonal Ruang

Diagonal ruang adalah garis yang menghubungkan dua titik sudut yang tidak sebidang. Perhatikan kubus berikut.

Diagonal ruang pada kubus ABCD.EFGH di atas adalah AG. Anda bisa menyebutkan diagonal ruang lainnya. Ada berapa semua diagonal ruang kubus?

Contoh 2.

Hitunglah panjang diagonal ruang AG pada kubus ABCD.EFGH yang memiliki panjang rusuk 8 cm!

Penyelesaian.

Berikut ini gambar kubus ABCD.EFGH dan diagonal ruang AG.

Diagonal ruang AG berada pada segitiga ACG, dengan siku-siku di titik C. 

Dari Contoh 1, diperoleh panjang AC adalah $8\sqrt{2}$ cm. Dengan menerapkan teorema Phytagoras, diperoleh:

\begin{array}{rcl} AG^{2}&=&AC^{2}+CG^{2} \\ AG^{2}&=&\left ( 8\sqrt{2} \right )^{2}+8^{2}\\ AG^{2}&=&128+64\\ AG^{2}&=&192\\ AG&=&\sqrt{192}\\ AC&=&8\sqrt{3}\\\end{array}  

Jadi, panjang diagonal ruang AG adalah $8\sqrt{3}$ cm.

Dengan cara yang sama, jika panjang rusuk kubus adalah $a$, maka diperoleh panjang diagonal ruang kubus adalah:

$\boxed {a\sqrt{3}}$

Latihan

1. Hitunglah panjang diagonal sisi kubus yang memiliki panjang rusuk 12 cm!
2. Panjang rusuk kubus ABCD.EFGH adalah 20 cm. Berapakah panjang diagonal ruang kubus tersebut?
3. Kubus PQRS.TUVW memiliki panjang diagonal sisi $10\sqrt{2}$ cm. Berapakah volume kubus tersebut?

Share :